Matlab 2

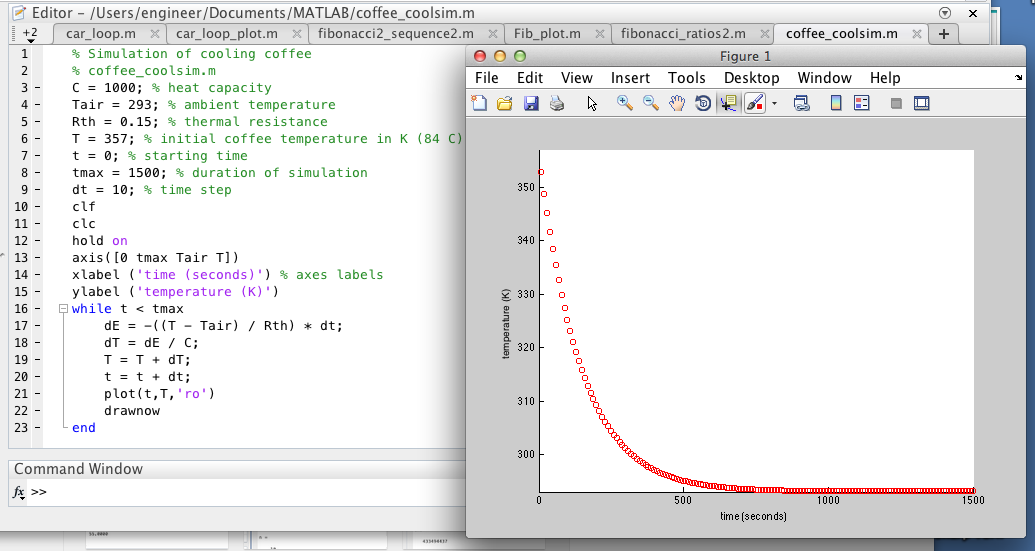
To further our understanding about MATLAB, we had to show a code that simulates how a cup of coffee cools to room temperature. The code and resulting graph. The graph plots time on the x axis and the temperature of the coffee on the y axis. Note all temperature is in Kelvin.

Question 1: How does the cooling behavior change if we vary the parameters Rth (thermal resistance) and C (heat capacity)?

 If you increase Rth and C, the coffee will retain more heat and the graph will decrease slower and the coffee will stay hot longer.

Rth increased from .8 to 2.85 while C stayed the same.

Rth stayed the same, while C increased from 1000 to 2000

Rth increased from .85 to 2.85 and C increased from 1000 to 2000

On the other hand, if C and Rth decrease, the coffee will not retain heat as well and the coffee will cool off much quicker.

Rth decreased from .85 to .15 while C stayed the same

Rth stayed the same, while C decreased from 1000 to 100

Rth decreased from .85 to .15 while C decreased from 1000 to 100

Then we needed to add a heater to the coffee. If the coffee started at room temperature and turn the heating element on, the element would add thermal energy to the system at a constant rate P.

Question 2: Calculate the value for P if we want our coffee to heat up to the Starbucks ideal of 84 degrees Celsius or 357 Kelvin?

P=75.29- We were given an equation in class and we then solved it to find this number

Once we found P, we needed to incorporate P into our program to see how it would affect the system. Over time, the coffee heated up to the desired temperature.

Then, we needed to modify the program to simulate a temperature controller that uses bang-bang control to reach and maintain the desired temperature.

Below is a zoomed in version of the graph.

Page 9. Question 1: Why is bang-bang control appropriate for many thermal systems? When might it be insufficient?

It is appropriate for thermal systems because it heats up to the desired temperature as fast as possible and is also cheap and easy to implement. The reason why our proportional control heated up faster than our bang bang control was because the max power in our proportional control is a lot larger than our max power in our bang bang control. However, it could be insufficient if it would be detrimental if the temperature went above the desired temperature as bang-bang control will ends up going a small amount over the desired temperature.  

Then we needed to create a program that uses proportional control to reach and maintain the desired temperature.

Page 9. Question 2: How does this approach compare to bang-bang?

This approach never reaches the desired value, though it does get very close.

After, we assumed that there was a delay between the time the coffee reaches a given temperature and when the temperature sensor records that temperature. We needed to modify both of of our programs to include the affect of adding a "sensor delay".

Bang Bang Control

The impact of the sensor delay is that the temperature gets read 5 seconds after it was initially read. Because of the delay, the first 5 seconds of the graph show a temperature of 293. It also doesn't turn the power on as often since it records temperature of the coffee 5 seconds after it reads the temperature.

Proportional Delay

The sensor delay has the effect that the temperature gets recorded 5 seconds after it was initially read. Therefore, the first 5 seconds of the graph are at a temperature of 293. The temperature also goes over the desired temperature since it records the temperature 5 seconds after it has read it. Then the system will turn off the power after it has gone over the desired temperature by 5 seconds.

Question2: What other delay(s) might you expect in your thermodynamic system, apart from sensor delays? 

One other delay can be an action delay. There could be a delay when the power is supposed to turn on to when it actually turns on.

Reflection:

I completely understand bang bang and proportional control now. It took us a long time to do the last problem with the delay because of small syntax errors. So I know that it is important reread the code to fix all errors.